数学物理有何关联及应用前景如何？

安德鲁 2025年02月19日 03:01 20 0

数学和物理，就像是一对紧密相连的好伙伴，在科学的世界里携手前行，它们相互依存、相互促进，共同推动着人类对自然规律的探索和科技的进步，数学物理究竟有着怎样的奥秘呢？就让我们一起深入探究一下。

数学物理的定义与内涵

数学物理可不是简单地把数学和物理拼凑在一起哦。数学物理是一门交叉学科，它运用数学的方法来研究物理问题，同时也从物理现象中汲取灵感，推动数学的发展，比如说，在研究物体的运动时，我们可以用数学中的函数来描述物体的位置、速度和加速度随时间的变化关系。

数学物理有何关联及应用前景如何？

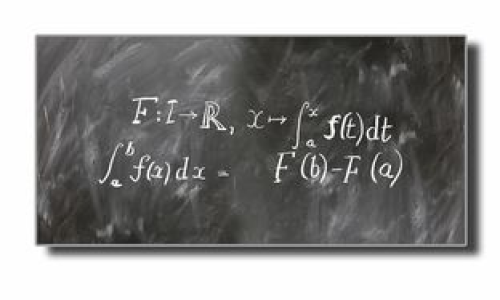
从内涵上来说，数学物理强调的是数学和物理之间的内在联系，它不仅仅是用数学公式来表达物理规律，更重要的是通过数学的逻辑推理和分析，揭示物理现象背后的本质，就像在研究电磁场时，麦克斯韦方程组用简洁而优美的数学形式，准确地描述了电场和磁场的相互关系和变化规律。

数学物理的发展可以追溯到古代，古希腊时期，阿基米德就运用数学方法研究了浮力原理和杠杆原理，这可以看作是数学物理的早期萌芽，在那个时候，人们就已经开始意识到数学和物理之间的紧密联系了。

到了近代，牛顿和莱布尼茨发明了微积分，这为数学物理的发展带来了巨大的飞跃，牛顿用微积分来研究物体的运动和万有引力定律，成功地解释了天体的运行规律，微积分的出现，让人们能够更加精确地描述和分析物理现象。

随着时间的推移，数学物理不断发展壮大，在19世纪和20世纪，麦克斯韦建立了电磁场理论，爱因斯坦提出了相对论，量子力学也应运而生，这些伟大的理论成果，都是数学物理发展的重要里程碑，它们不仅深刻地改变了人们对自然界的认识，也推动了现代科技的飞速发展。

数学在物理中的应用那可是无处不在的，在力学中，我们用牛顿第二定律\(F = ma\)来描述物体的受力和运动状态的关系，这个简单的公式，却蕴含着深刻的物理意义，它就像是一把钥匙，能够帮助我们打开物体运动奥秘的大门。

在电磁学中，数学的应用更是至关重要，麦克斯韦方程组就是用数学语言来描述电场和磁场的变化规律，通过对麦克斯韦方程组的求解，我们可以预测电磁波的存在和传播特性，这为现代通信技术的发展奠定了基础。

在量子力学中，数学的作用更加突出，量子力学中的波函数、算符等概念，都需要用高深的数学知识来描述和理解，比如说，薛定谔方程就是量子力学中的一个核心方程，它用数学的方式描述了微观粒子的运动状态。

物理不仅仅是数学的应用对象，它还对数学的发展起到了重要的推动作用，物理问题的复杂性和多样性，常常促使数学家们去开发新的数学方法和理论。

在研究流体力学中的湍流问题时，传统的数学方法遇到了很大的困难，为了解决这个问题，数学家们发展了分形几何和混沌理论等新的数学分支，这些新的数学理论不仅为解决物理问题提供了有力的工具，也丰富了数学的内涵。

物理实验中的数据处理和分析也对数学提出了新的要求，为了从大量的实验数据中提取有用的信息，数学家们发展了统计学和概率论等学科，这些学科在现代科学和工程领域中有着广泛的应用。

在现代科技中，数学物理的应用可谓是无处不在，在计算机科学中，数学物理的知识被广泛应用于算法设计、图形处理和人工智能等领域，比如说，在计算机图形学中，我们需要用数学方法来描述和渲染三维物体，这就需要用到线性代数和微积分等知识。

在医学领域，数学物理的应用也越来越重要，医学成像技术，如CT扫描、核磁共振等，都离不开数学物理的原理，通过对这些成像技术的研究和改进，医生们能够更加准确地诊断疾病，为患者提供更好的治疗方案。

在能源领域，数学物理的知识对于开发新能源和提高能源利用效率也有着重要的作用，在研究太阳能电池和风力发电机的性能时，我们需要用数学模型来描述和优化它们的工作过程。

数学物理有何关联及应用前景如何？

学习数学物理可不是一件容易的事情，需要掌握一些方法和技巧，要打好数学和物理的基础，数学是物理的工具，只有掌握了扎实的数学知识，才能更好地理解和应用物理原理。

要注重理论和实践相结合，在学习数学物理的过程中，不仅要学习理论知识，还要通过做实验和解决实际问题来加深对知识的理解和掌握，比如说，在学习力学时，可以通过做一些简单的力学实验，如弹簧振子实验、单摆实验等，来直观地感受物理现象和规律。

要善于总结和归纳，数学物理中的知识点很多，而且相互之间有着密切的联系，通过总结和归纳，可以将所学的知识系统化，形成一个完整的知识体系，比如说，在学习电磁学时，可以将电场、磁场、电磁感应等知识点进行总结和归纳，找出它们之间的联系和区别。

尽管数学物理在过去取得了巨大的成就，但它仍然面临着一些挑战，比如说，在研究一些复杂的物理系统时，如生物系统、生态系统等，现有的数学方法还不能完全满足需求，这就需要数学家和物理学家们共同努力，开发新的数学方法和理论。

随着科技的不断发展，数学物理也面临着新的机遇和挑战，在量子计算、人工智能等领域的发展，为数学物理的研究提供了新的方向和动力，这些领域的发展也对数学物理的理论和方法提出了更高的要求。

展望未来，数学物理有着广阔的发展前景，它将继续在科学研究和技术创新中发挥重要的作用，我们相信，在数学家和物理学家们的共同努力下，数学物理将会取得更加辉煌的成就，为人类的进步和发展做出更大的贡献。